其实说起来误差和不确定度,确实是灰常容易混淆的指标。学霸们可能还依稀记得,估计不常接触的亲们基本都忘了。下面帮大家温习一下:
误差实际上是指测量值与真值之差,一般来说我们认为误差是可以被修正掉的。比如误差的两大组成部分系统误差和随机误差,系统误差可以从理论、改进实验装置、测试方法等修正掉;随机误差可以通过增加测量次数、重复测量的算术平均值等消除。
而不确定度是表征被测量量值分散性的情况,形象来说不确定度理论认为真值是无法通过测量得到的,因此每一次测量中都会存在一部分不确定性,这里面包含了各种因素,也就是不确定度分量,只有无穷次测量的平均值才能无限趋近于真值,公式中的无论是测得值,真值,标称值实际上都不能真正得到,得到的只是一个近似值,参见咱们量子力学中著名的“测不准原理”。看晕了的筒子们可以直接看下表:
|
类型 |
测量误差 | 测量不确定度 |
| 含义 | 表明测试结果偏离真值的程度 | 表明被测量值的分散性 |
| 分类 | 按性质分为随机误差和系统误差两类 | 按评定方法分为A,B两类 |
| 主客观性 | 客观存在,不以人的认知度而改变 | 与对被测量、影响量及过程的认知有关 |
| 置信概率 | 不需要且不存在 | 需要且存在 |
| 与分布的关系 | 无关 | 有关 |
表一、测量误差和不确定度的区别
总而言之,误差都是可以修正掉的,但是不确定度是个概率事件,是无法修正掉的。
关于不确定度的详细理解,大家可以参考下面的一张图:
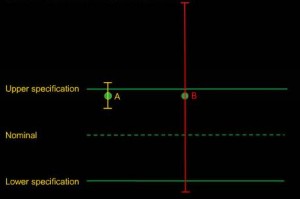
图一、不同不确定度测量值的比较
A和B为两个相等的测试值,但是A的不确定度小,B的不确定度大。我们可以认为加上测试不确定度后,A的真值区间比较小,B的真值区间比较大。因此,A相对于B来讲,超标的概率更低,测试结果更加可信。
上述的不确定度分布区间,一般来说,我们在做不确定度分析的时候,采用比较多的都是统计因子等于2,为95%的一个置信概率。测试不确定度在测试中最常见的领域是校准,有些非常严谨的测试系统建立的时候也会评估其不确定度,除此以外别的领域也见得不多。
那肿么神秘的测量不确定度是怎么算出来的呢?一般国际通行的是用GUM(全称Guide to the Uncertainty in Measurement,简称GUM)。下面的具体步骤一般筒子可以省略,科学帝们可以继续J
1. 明确被测量。
2. 测量方程:将被测量与其他相关参量进行数学建模,得到测量方程。
3. 不确定度方程:对测量方程进行推导,考虑各项不确定度来源在其中的贡献,得到不确定度方程。
4. 不确定度:将各个参量的数值带入测量方程和不确定度方程,求得测量不确定度。
步骤是不是很复杂?嘿嘿,算不确定度可是个高级职位,英文名Metrologist,中文名计量学家,估计在电子行业的地位类似于保险精算师,这份钱可不是白拿的。肿么样,又长见识了吧?哈哈。
所以呢,一般来讲,在比较靠谱的校准实验室,最后出的校准报告是长这个样子的(借用前A家现K家的美美滴测试报告):
所以亲们可以回去看一下啊,你的仪表校准报告带不确定度了么J
这期测量误差和不确定度的大坑就给大家补到这里,咱们节后继续哦!