在RF/微波领域,为了实现电磁信号的连续传输,经常需要将多个无源/有源器件级联起来。特别是,在连接具有不同接口的子系统、模块时,大量用到各种各样的转接器件。一个看似简单却又难倒许多入门者的问题是:多个器件级联后总的传输特性与每个器件各自的传输特性究竟有什么关系?前阵子,朱辉老师在群里出了一个趣味题,可能就是两个无源器件级联后的传输特性与级联前的传输特性关系问题。下面,本文以滤波器串联为例浅论下此问题,抛砖引玉。
本人初入门做微波测试时,曾经想要获得一个具有相对较高带外抑制度的低通滤波器,便天真地想到用两个低通滤波器级联的方法。例如,预计要获得60dB的带外抑制,而手里头只有若干个带外抑制为40dB左右的低通滤波器。于是,按照直观的信号衰减理解,当将两个40dB带外抑制的滤波器串联起来时,信号经过第一个滤波器会衰减40dB,紧接着经过第二个滤波器时同样也会衰减40dB,大功告成——总共可衰减80dB!于是兴高采烈地搭建电路做测试,结果发现:信号经过两个串联的滤波器后,其衰减远小于80dB。当时一直不能理解,也不知道应该运用微波工程教科书里的S参数级联理论来分析这个问题。直到后来摸爬滚打许久后,才恍然大悟这个问题原来教科书上有理论描述。不免感叹:纸上得来终觉浅,绝知此事要躬行。
实际上,在几乎所有的微波工程教科书中“微波网络分析”章节中都会讲到:每个无源器件的电特性都可以运用四种网络参数来描述:S、Z、Y、ABCD参数,并且这四种参数之间可以相互转换。通常,我们都用S参数来描述无源器件的电特性,依据S参数与ABCD参数间的相互转化关系,可以方便地得到ABCD参数;而当多个无源器件级联时,总的ABCD参数是各级联无源器件ABCD参数的矩阵乘积。总而言之,当知道被级联的多个无源器件的S参数时,首先将S参数转换为ABCD参数,然后将各器件的ABCD参数矩阵相乘得到级联后的ABCD参数,最后再将总的ABCD参数转换为S参数便得到了多个无源器件级联的总的S参数。
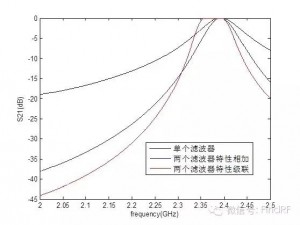
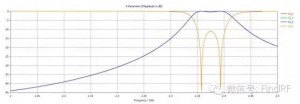
按照这个思路,对两个滤波器的级联特性进行了计算,结果如图1所示。图1中,黑线为单个滤波器的S21特性(假设串联的两个滤波器特性完全一样);蓝线是按照“衰减加和”思想得到的两个滤波器级联后S21特性,可以看到,此时在任意频点处衰减加倍;红线是中规中矩地按照微波网络分析理论计算得到的两个滤波器级联S21,可以看到,从信号的衰减角度来看,在低频段和高频段,级联S21的衰减大于“衰减加和”得到的衰减(“衰减加和”的思想低估了级联后的衰减),但在中间频段,级联S21的衰减小于“衰减加和”得到的衰减(“衰减加和”的思想高估了级联后的衰减)。因此,电磁信号经过多个串联的器件时,其衰减可能大于各器件衰减之和,也可能小于各器件衰减之和。
图1 按照ABCD矩阵级联得到的两个滤波器串联特性(解析计算)
有了上述理论认识后,就对前述“串联低通滤波器的衰减”问题不是那么丈二和尚摸不着头脑了。
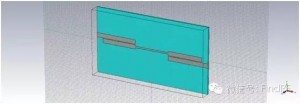
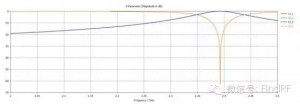
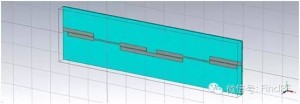
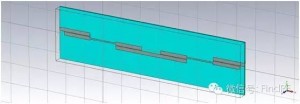
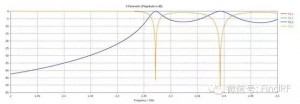
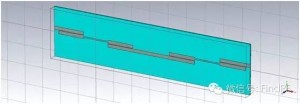
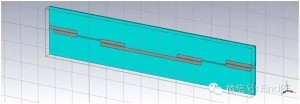
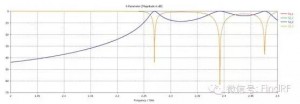
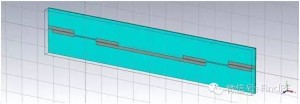
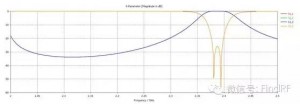
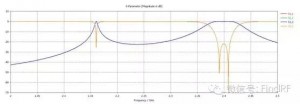
上面采用微波网络分析理论对滤波器的串联进行了解析分析,下面运用电磁仿真软件对此做进一步验证和探讨。图2、3给出了单个滤波器的模型及仿真结果,图4、5给出了两个相同的滤波器串联后的模型及仿真结果,图6、7、8、9、10则分别给出了在两个串联滤波器中间加入长度为10、30、50、70、100mm传输线时的模型及仿真结果。可以看到,图5给出的仿真结果与图1中得到的计算结果是一致的;滤波器串联后,衰减特性与频率有关;两个滤波器之间插入的传输线长度对级联后的S21有显著影响。
例如:图2显示单个滤波器在2.4GHz处回损约15dB;图5、6、7、8、9、10显示串联后回损约12、10、20、10、18、22dB;可见,就该频点来看,串联后的回损可能优于单个器件的回损、也可能劣于单个器件的回损。
图6 两个滤波器之间引入10mm的微带线及其仿真结果
图7 两个滤波器之间引入30mm的微带线及其仿真结果
图8 两个滤波器之间引入50mm的微带线及其仿真结果
图9 两个滤波器之间引入70mm的微带线及其仿真结果
图10 两个滤波器之间引入100mm的微带线及其仿真结果
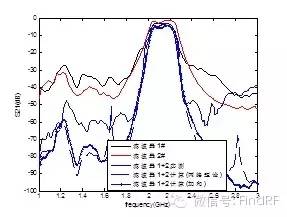
利用自制微带滤波器进行了级联的实验验证:首先,分别测量两个滤波器的S参数;然后,将这两个滤波器级联后测试总的S参数。图11-图13给出了所测滤波器实物图。图14给出了单个滤波器和级联滤波器的S21测试结果,作为对比,同时给出了采用前述网络理论以及简单加和方法得到的级联滤波器S21。可以看到:在中心频率附近,级联滤波器的传输特性测试结果与理论分析基本吻合;但是在带外部分,所测抑制度小于理论抑制度,并且采用网络理论与简单加和法得到的计算结果基本一致。工艺与测试可能是造成理论与实测有一定偏差的原因。
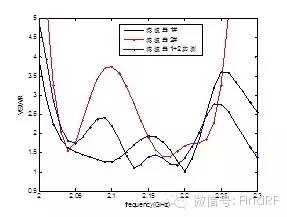
图15给出了驻波比级联的测试结果:级联后的驻波比可能优于级联前的驻波比,也可能劣于,具体取决于观察频点。观察图15上图,在3GHz频点,级联后的驻波比低于1.5,显著优于级联前的频点;从图15结果来看,级联后的驻波比总体上优于或相当于级联前的驻波比,但图5下图低频部分显示:级联后的驻波比劣于级联前的驻波比。
图15 级联滤波器的驻波比(上图是端口1驻波比,下图是端口2驻波比)
以滤波器串联为例分析了无源器件串联后的传输特性,结果表明串联后的回损是否优于或劣于串联前单个器件的回损,是与具体频点相关的。这一点,本文给出的理论结果与实验结果均证实这一规律。
由于滤波器属于谐振器件,自身具有特殊性,后续将以常见的同轴转接器为对象,进一步探讨无源器件的串联话题。
作者简介:叶鸣,西安交通大学微电子学院讲师,研究兴趣包括射频/微波无源器件/电路设计及其应用,无源互调等。